حوزههای کمی از ریاضیات به اندازه حساب دیفرانسیل و انتگرال در توصیف و تحلیل دنیای فیزیکی مفید هستند. این حوزه را میتوان مطالعه ریاضی تغییرات نامگذاری کرد. حساب دیفرانسیل و انتگرال همچنین برای اکثر افرادی که در ابتدا با آن مواجه میشوند، میتواند بسیار گیجکننده باشد. بخشی از این گیجکنندگی میتواند از اصرار ریاضیدانان بر انکار شهودی بودن این حوزه باشد.
سیلوانوس پی. تامپسون، در کتاب حساب دیفرانسیل و انتگرال ساده که در سال 1910 منتشر شد، متن خود را با فصلی کوتاه با عنوان «رهایی شما از وحشتهای اولیه» آغاز کرد. در این مقالات ما از او پیروی خواهیم کرد و به طور مشابه شما را با برخی از نمادهایی که اغلب در حساب دیفرانسیل و انتگرال استفاده می شود، همراه با تعاریف بسیار ساده (البته نه از نظر ریاضی دقیق) آشنا می کنیم.
هنگامی که میخواهیم از تغییر در مقدار یک متغیر صحبت کنیم (مثلاً x)، معمول است که قبل از متغیر با حرف بزرگ یونانی "delta" قرار داده شود:
Δx = "Change in x"
به جای کلمه “Delta” میتوان از نماد آن (Δ) استفاده نمود. با این حساب Δx به عنوان تفاوت بین دو مقدار x میباشد. علت این تفاوت مهم نیست. ممکن است این تفاوت بین ۲ زمان یا دو نقطه از فضا باشد.
برای مثال اگر دمای یک کوره (T) در طول زمان افزایش یابد، ممکن است بخواهیم آن تغییر دما را به عنوان ΔT توصیف کنیم.
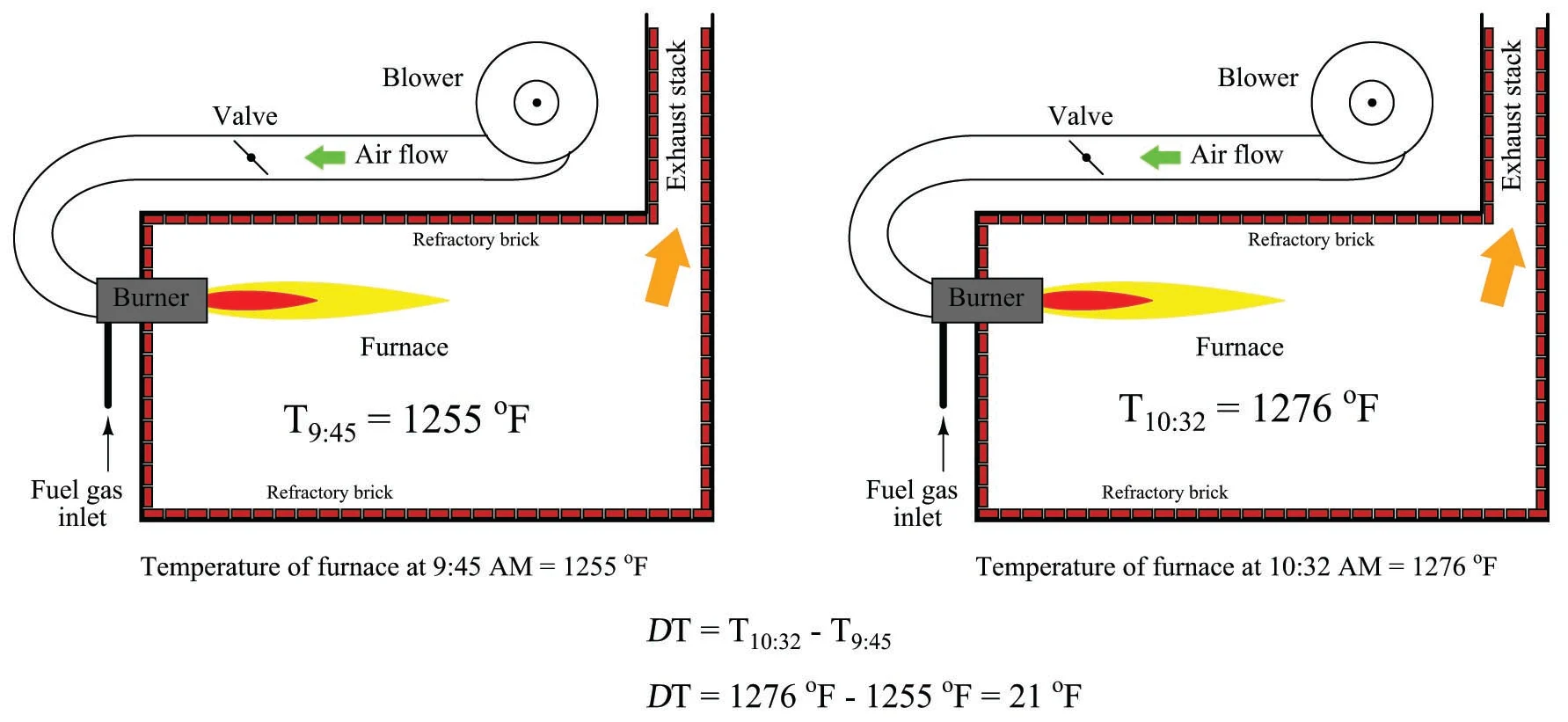
مقدار ΔT چیزی بیش از تفاوت بین دمای اخیر و دمای قدیمیتر نیست. بنابراین افزایش دما در طول زمان یک مقدار مثبت برای ΔT به ما میدهد، در حالی که کاهش دما در طول زمان یک مقدار منفی برای ΔT به ما میدهد. همچنین میتوانیم تفاوتهای بین دمای دو مکان را با علامت ΔT توصیف کنیم، مانند این مثال از انتقال حرارت از طریق یک دیوار رسانای گرما که در آن یک طرف دیوار داغتر از طرف دیگر است:

یک بار دیگر، ΔT با کم کردن یک دما از دمای دیگر محاسبه می شود. در اینجا علامت (مثبت یا منفی) ΔT نشان دهنده جهت جریان گرما است.
یکی از نگرانیهای اصلی حساب دیفرانسیل و انتگرال، تغییر یا تفاوت بین مقادیر متغیر است که بسیار نزدیک به یکدیگر قرار دارند. در زمینه یک کوره گرمایش، این می تواند به معنای افزایش دما در دورههای زمانی کوچک باشد. در زمینه جریان گرما از یک دیوار، این می تواند به معنای تفاوت در دمای نمونه برداری شده بین نقاط داخل دیوار بلافاصله در مجاورت یکدیگر باشد. اگر تمایل ما این است که تغییر در متغیری را بین نقاط همسایه در امتداد یک پیوستار به جای یک دوره گسسته بیان کنیم، ممکن است از حرف دلتا (Δ) استفاده نکنیم و به جای آن از حرف کوچک آن استفاده کنیم. (δ)
بنابراین، تغییر دمای کوره از یک لحظه به لحظه دیگر می تواند به صورت dT (یا δT) بیان شود، و به همین ترتیب، تفاوت دما بین دو موقعیت مجاور در دیواره رسانای گرما نیز می تواند به صورت dT (یا δT) بیان شود. درست مانند نماد "دلتا" (Δ)، ارجاعات تغییر توسط d یا δ ممکن است در دامنههای مختلف رخ دهد.
ما حتی یک نام منحصر به فرد برای مفهوم تفاوت های بسیار کوچک داریم: در حالی که ΔT را اختلاف دما می نامند، dT را دیفرانسیل دما می نامند. مفهوم دیفرانسیل ممکن است در حال حاضر برای شما زائد به نظر برسد، اما آنها در واقع برای توصیف تغییرات پیوسته بسیار قدرتمند هستند، به خصوص زمانی که یک دیفرانسیل با نسبت دیگر به دیفرانسیل دیگر مرتبط باشد (چیزی که ما مشتق می نامیم).
یکی دیگر از نگرانی های اصلی در حساب دیفرانسیل و انتگرال این است که چگونه کمیت ها انباشته می شوند، به ویژه اینکه چگونه کمیت های دیفرانسیل جمع می شوند تا یک کل بزرگتر را تشکیل دهند. برای مثال، افزایش دمای کوره از زمان راه اندازی (ΔTtotal) را میتوان به صورت مجموع بسیاری از تفاوتهای دما (ΔT) که به صورت دورهای اندازهگیری میشود، بیان کرد. کل افزایش دمای کوره محاسبه شده از یک نمونهگیری دما یک بار در دقیقه از ساعت 9:45 تا 10:32 صبح را می توان به صورت زیر نوشت:
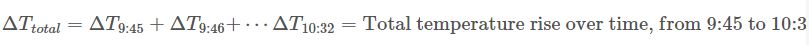
اگر بخواهیم این عبارت را به زبان ریاضی بنویسیم، از سیگما استفاده میکنیم.

با این حال، اگر مانیتور دمای کوره ما با سرعت بینهایت اسکن کند، تفاوتهای دما (dT)) را اندازهگیری کند و آنها را پشت سر هم جمع کند، ممکن است همان افزایش دمای انباشتهشده را بهعنوان مجموع بینهایت تغییرات بینهایت کوچک (بینهایت کوچک) بیان کنیم. مجموع محدودی از تغییرات دما که هر دقیقه یک بار اندازه گیری می شود. همانطور که ما یک نماد ریاضی منحصر به فرد را برای نشان دادن دیفرانسیل های (d) در یک پیوستار به جای تفاوت ها (Δ) در دوره های گسسته معرفی کردیم، یک نماد ریاضی منحصر به فرد را برای نشان دادن جمع دیفرانسیل ها (∑) به جای مجموع تفاوت ها معرفی خواهیم کرد.(∫)
