مفهوم مشتق‌گیری

فرض کنید می‌خواهیم سرعت جریان گاز پروپان را از طریق شیلنگ به مشعل اندازه‌گیری کنیم:

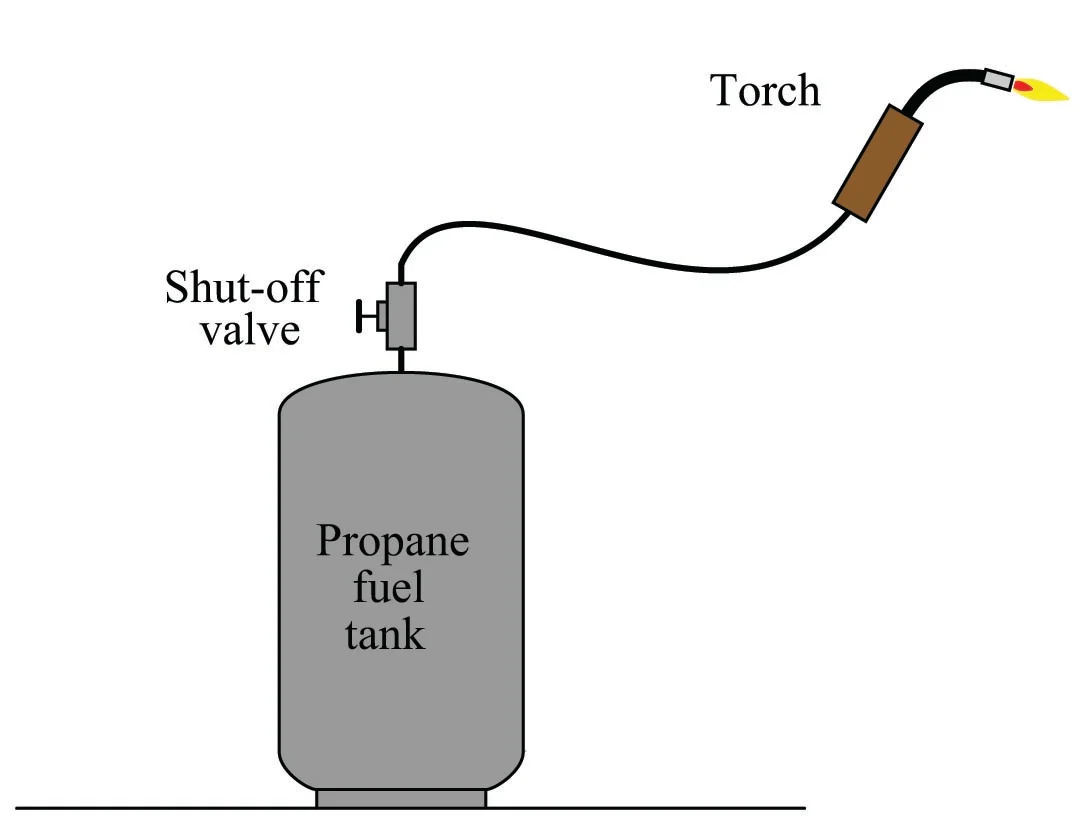
فلومترهای مناسب برای اندازه‌گیری دبی پایین هر گاز معمولاً بسیار گران هستند و اندازه‌گیری مستقیم دبی گاز سوخت پروپان مصرف شده توسط این مشعل در هر لحظه را غیر منطقی می‌کند. با این‌حال، می‌توانیم به‌طور غیرمستقیم نرخ جریان پروپان را با قرار دادن مخزن در مقیاسی اندازه‌گیری کنیم که جرم آن (m) در طول زمان قابل نظارت باشد. با اندازه‌گیری جرم در بازه‌های زمانی کوتاه (Δt)، می‌توانیم تفاوت‌های مربوطه را در جرم (Δm) محاسبه کنیم، سپس نسبت جرم از دست رفته در طول زمان را برای محاسبه متوسط دبی جرمی محاسبه کنیم:

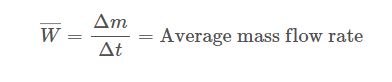
W = متوسط دبی جرمی در هر دوره زمانی (کیلوگرم در دقیقه)

Δm = اختلاف جرم اندازه گیری شده در طول دوره زمانی (کیلوگرم)

Δt = دوره زمانی اندازه‌گیری (دقیقه)

توجه داشته باشید که نرخ جریان (Flow) نسبت (ضریب) تغییر جرم در طول تغییر زمان است. واحدهای مورد استفاده برای بیان جریان نیز این موضوع را تایید می‌کند: کیلوگرم در دقیقه. 

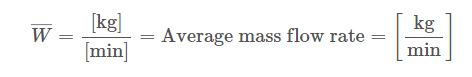
به عنوان یک تابع در طول زمان، جرم مخزن با گذشت زمان کاهش می یابد. هر نقطه نشان دهنده یک جفت مختصات اندازه گیری جرم و زمان است (به عنوان مثال 20 کیلوگرم در 7:38، 18.6 کیلوگرم در 7:51 و غیره):

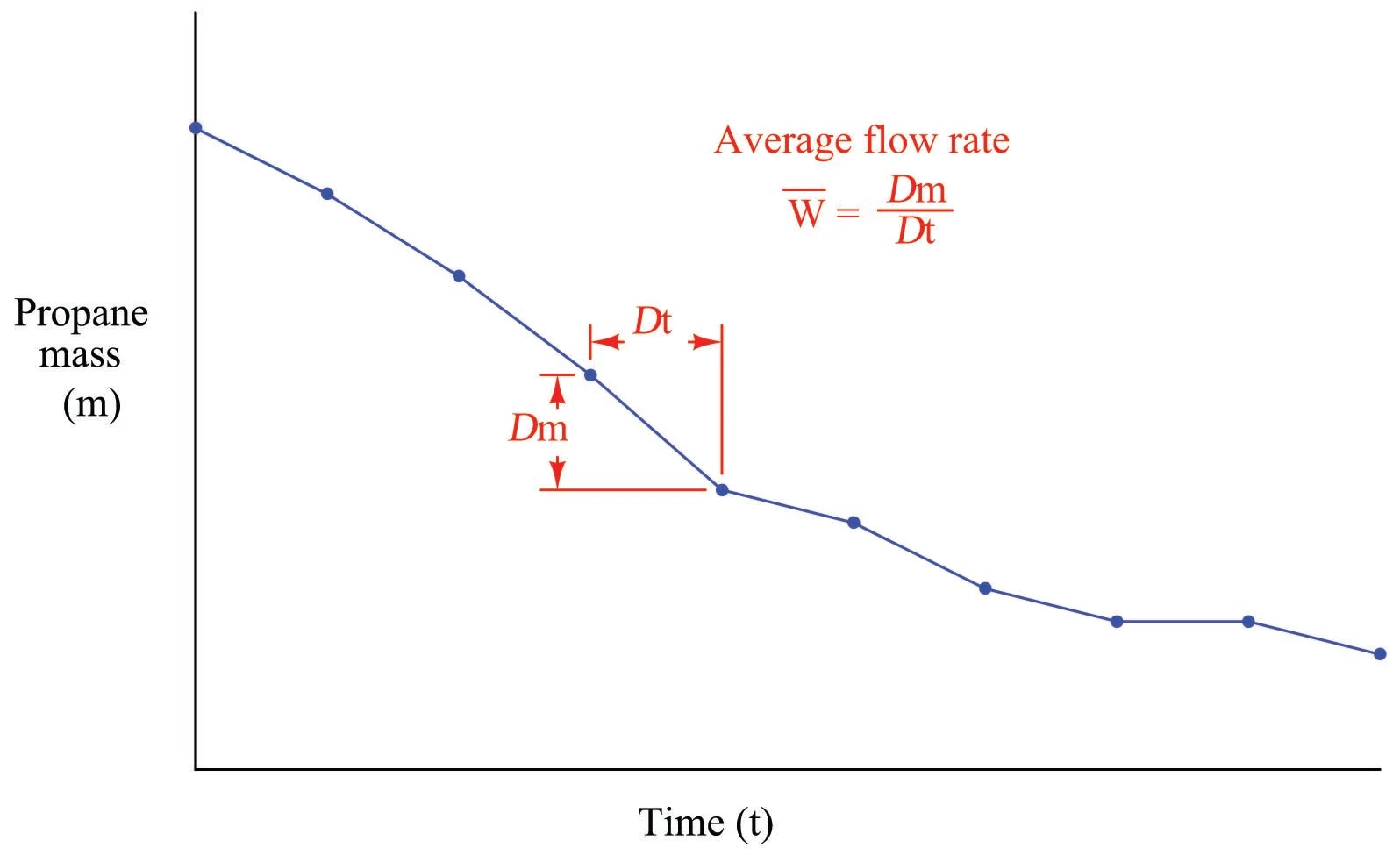
بر اساس قوانین هندسه شیب در یک نمودار با تقسیم ارتفاع به عرض تعریف می شود. بنابراین، متوسط دبی جرمی محاسبه‌شده در هر دوره زمانی ممکن است به‌عنوان شیب بخش‌های خطی که نقاط را به هم متصل می‌کنند، نشان داده شود، زیرا دبی جرمی به‌عنوان تغییر جرم به ازای تغییر در زمان تعریف می‌شود.

زمانی که شعله مشعل بزرگ باشد، شیب جریان پروپان زیاد شده و بالعکس در زمان کم شدن یا خاموش شدن این شعله، شیب نمودار مسطح می‌شود.

اگر تعیین نرخ متوسط جریان  برای ما به کافی باشد، نیازی به انجام کار بیشتری نداریم. با این حال، اگر بخواهیم نرخ جریان جرم را در هر لحظه خاص در زمان تشخیص دهیم، باید همان اندازه‌گیری‌های کاهش جرم، سپری شدن زمان و تقسیم این دو را با سرعت بی‌نهایت انجام دهیم.

با فرض اینکه چنین چیزی امکان پذیر باشد، چیزی که در نهایت به آن می رسیم یک نمودار صاف است که جرم مصرف شده در طول زمان را نشان می دهد. به جای چند پاره خط که یک منحنی را می‌سازد، تعداد بی‌نهایت پاره خط کوتاه  به هم متصل می‌شوند تا یک منحنی یکپارچه را تشکیل دهند. نرخ جریان در هر نقطه خاص از زمان، نسبت اختلاف جرم و زمان (شیب تکه خط بی‌نهایت کوچک) در آن نقطه خواهد بود:

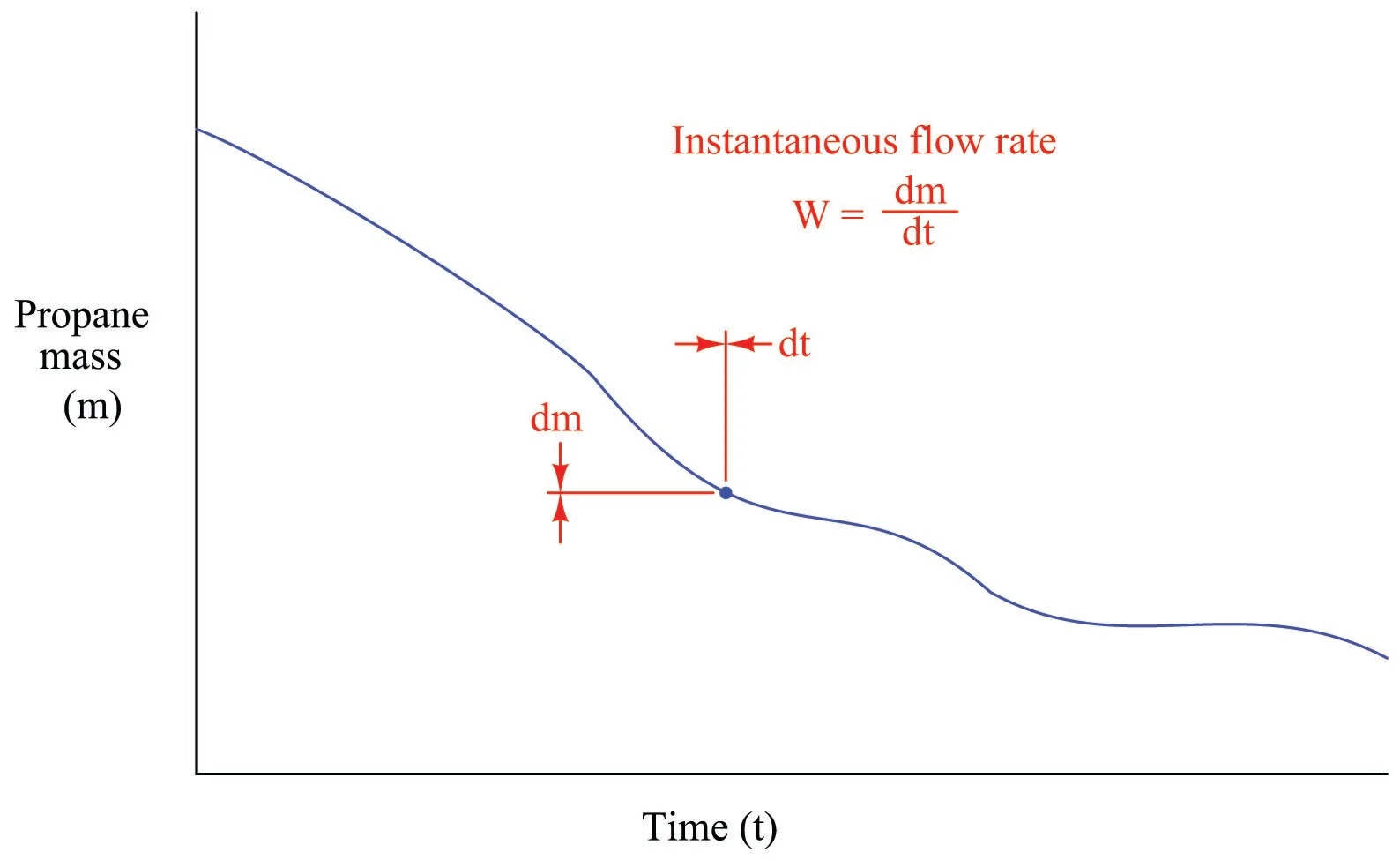
که در این فرمول:

W = سرعت جریان جرمی آنی در یک زمان معین (کیلوگرم در دقیقه)

dm = اختلاف جرم در یک نقطه زمانی (کیلوگرم)

dt = اختلاف زمان در یک نقطه از زمان (دقیقه)

جریان دقیقاً مانند قبل محاسبه می شود: ضریبی از اختلاف جرم و زمان، با این تفاوت که در اینجا تفاوت‌ها از بی‌نهایت کوچک هستند. درست مانند قبل، با سرعت جریان جرمی که بر حسب واحد کیلوگرم در دقیقه بیان می شود. همچنین، نرخ جریان به صورت گرافیکی با شیب نمودار نشان داده می‌شود: نقاط با شیب تند روی نمودار، جریان بالا را نشان می‌دهند، در حالی که نقاط با شیب کم روی نمودار،  جریان کم را نشان می‌دهند.

چنین نسبتی از مقادیر دیفرانسیل در حساب دیفرانسیل و انتگرال، مشتق نامیده می‌شود. مشتقات (به ویژه مشتقات مبتنی بر زمان مانند نرخ جریان) کاربردهای زیادی در ابزار دقیق و همچنین علوم عمومی دارند. برخی از متداول‌ترین توابع مشتق مبتنی بر زمان شامل روابط بین موقعیت (x)، سرعت (v) و شتاب (a) است.

واحدهای متریک اندازه‌گیری سرعت (متر بر ثانیه، مایل در ساعت و غیره) این روند تقسیم را نشان می دهند: دیفرانسیل موقعیت (متر) تقسیم بر دیفرانسیل زمان (ثانیه).

شتاب (a) نرخی است که یک جسم در طول زمان سرعت خود را تغییر می دهد. بنابراین، ممکن است شتاب را به عنوان مشتق زمانی سرعت بیان کنیم، همانطور که سرعت به عنوان مشتق زمانی موقعیت بیان شد:

ما حتی ممکن است شتاب را به عنوان تابعی از موقعیت (x) بیان کنیم، زیرا سرعت تغییر نرخ، تغییر موقعیت در طول زمان است. این به عنوان مشتق دوم شناخته می شود، زیرا فرآیند "تمایز" را دو بار اعمال می کند:

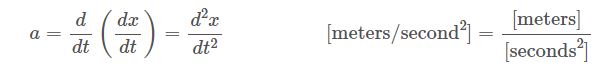
همانند سرعت، واحدهای اندازه گیری شتاب (متر بر ثانیه مجذور، یا متر بر ثانیه بر ثانیه) یک ضریب مرکب را پیشنهاد می کنند.

همچنین می توان نرخ های تغییر را بین متغیرهای مختلف بیان کرد که شامل زمان نمی شود. یک مثال رایج در حوزه مهندسی مفهوم بهره است که به طور کلی به عنوان نسبت تغییر خروجی به تغییر ورودی تعریف می شود. به عنوان مثال، تقویت‌کننده الکترونیکی با سیگنال ورودی 2 ولت (پیک به پیک) و سیگنال خروجی 8.6 ولت (پیک به پیک) دارای بهره 4.3 است، زیرا تغییر در خروجی اندازه گیری شده در ولت پیک به پیک 4.3 برابر بزرگتر از تغییر مربوطه در ولتاژ ورودی است:

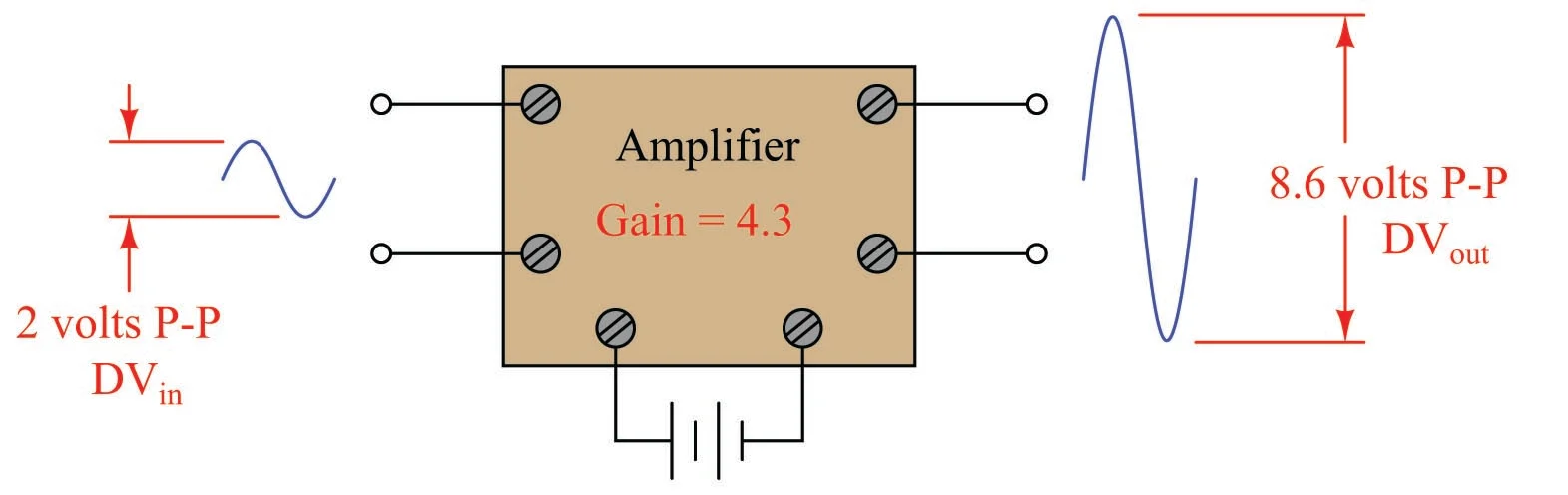
این سود ممکن است به عنوان یک ضریب تفاوت بیان شود، یا ممکن است به عنوان یک مشتق بیان شود:

اگر رفتار تقویت‌کننده کاملاً خطی باشد، هیچ تفاوتی بین بهره محاسبه‌شده با استفاده از تفاوت‌ها و بهره محاسبه‌شده با استفاده از دیفرانسیل (مشتق) وجود نخواهد داشت، زیرا میانگین شیب یک خط مستقیم با شیب آنی در هر نقطه از آن خط یکسان است. با این حال، اگر تقویت کننده به صورت کاملا خطی رفتار نکند، بهره محاسبه شده از تغییرات زیاد ولتاژ با بهره محاسبه شده از تغییرات بی نهایت کوچک در نقاط مختلف در امتداد محدوده ولتاژ کاری تقویت کننده یکسان نخواهد بود.